Research

Intro

My research primarily focuses on the numerical analysis of Finite Element Methods (FEM). Beyond standard techniques, I am particularly interested in advanced methodologies that incorporate structure-preserving properties, ensuring that critical physical or mathematical characteristics of the underlying problems are maintained. A key approach involves tailoring Finite Elements to the specific function spaces approaching in the continuous formulation of the problem. This ensures that the application of differential operators, such as the gradient, curl, or divergence, is well-defined and consistent. The corresponding numerical analysis is closely tied to the continuous theoretical framework, forming a mathematical exact sequence (complex) that offers clear insights and a solid foundation for understanding the problems.

While I have contributed to various projects involving second-order partial differential equations, my main passion lies in the numerical approximation and modeling of fluid dynamics.

Incompressible flows

A significant part of my research has been dedicated to the numerical approximation of incompressible flows. As the term suggests, incompressible fluids preserve mass due to the incompressibility constraint, making mass conservation a fundamental property of the system. A critical challenge in this field is ensuring that these physical properties are properly preserved in numerical approximations.

While various approaches exist, my work has primarily focused on H(div)-conforming methods within the framework of (Hybrid) discontinuous Galerkin methods and Mass-Conserving Stress-Yielding (MCS) methods. These approaches are designed to enforce local conservation properties and ensure the continuity of the normal components of fluxes across element boundaries. In this context, I have addressed key topics, including:

• Stability, approximation and optimization properties
• Mixed approaches including Non-Newtonian fluids
• Purous media flows and coupling to other transport equations
• Turbulence models such as implicit large eddy simulations (ILES)

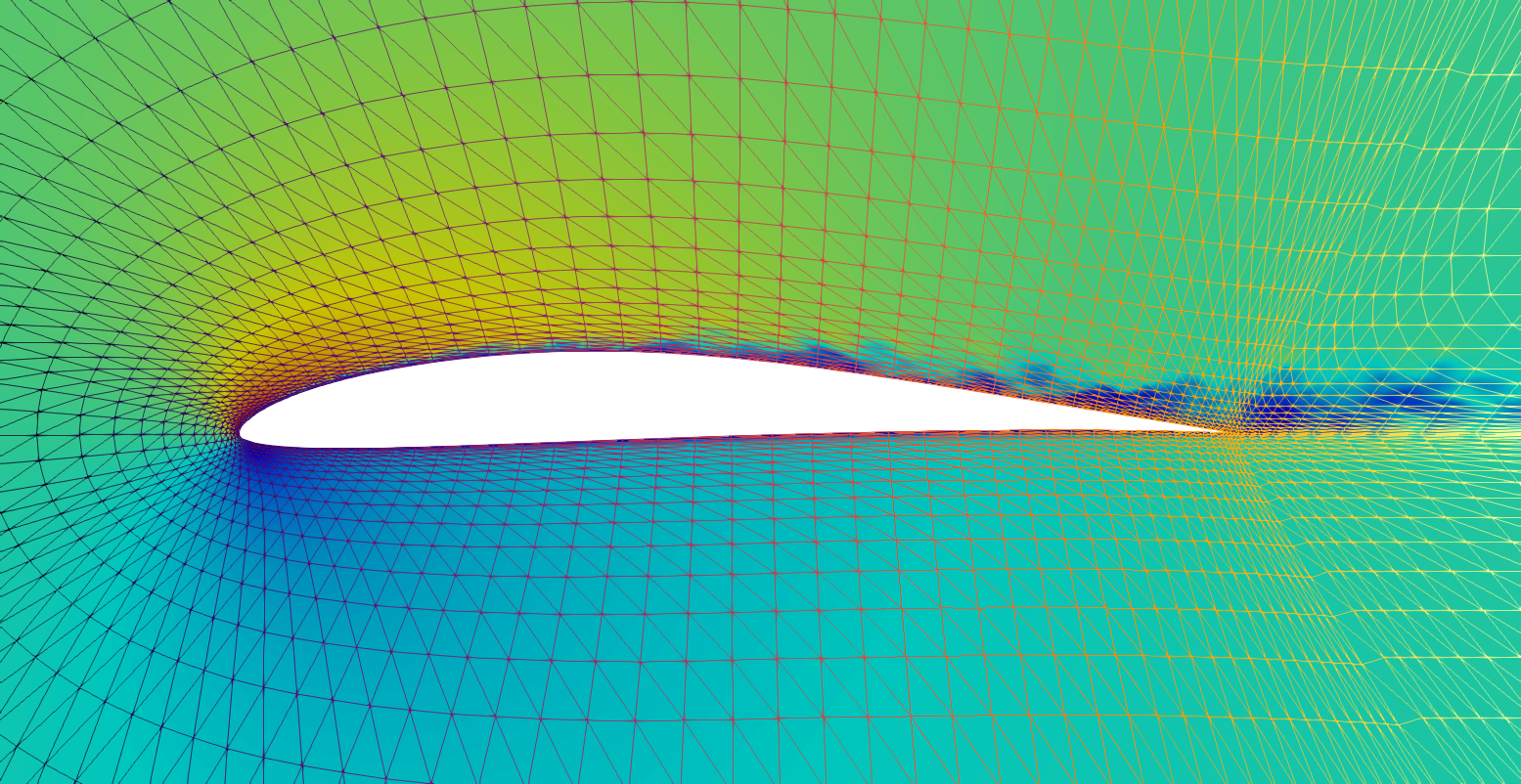
I have also worked on a posteriori error estimators, which involve the development and analysis of algorithms to quantify the approximation errors in simulations. These estimators provide rigorous error bounds, offering insights into the reliability of the numerical results. A significant application of this work is the derivation of adaptive mesh refinement techniques, where finer meshes are generated locally in regions with higher approximation errors. This approach improves the accuracy of the solution while optimizing computational resources by concentrating effort where it is most needed.

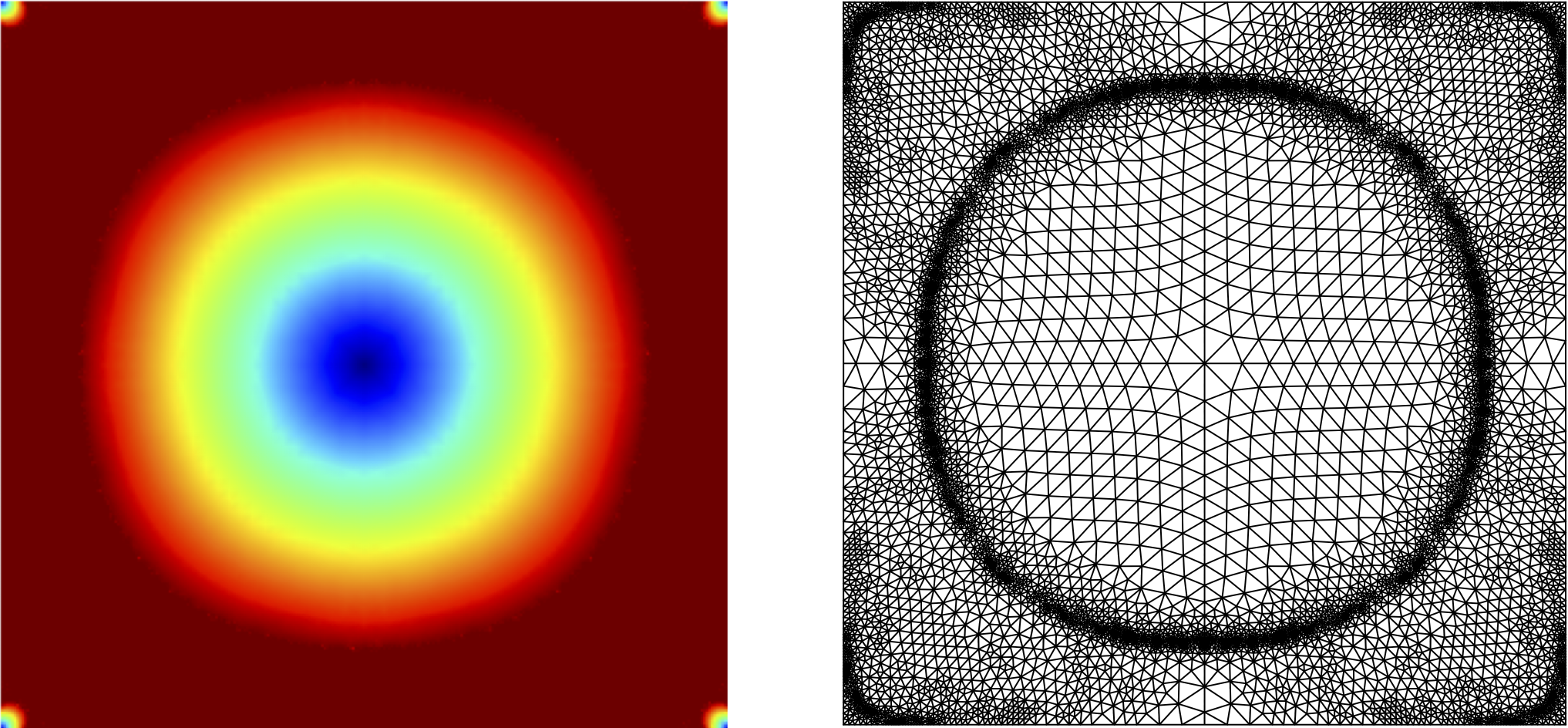
Compressible flows

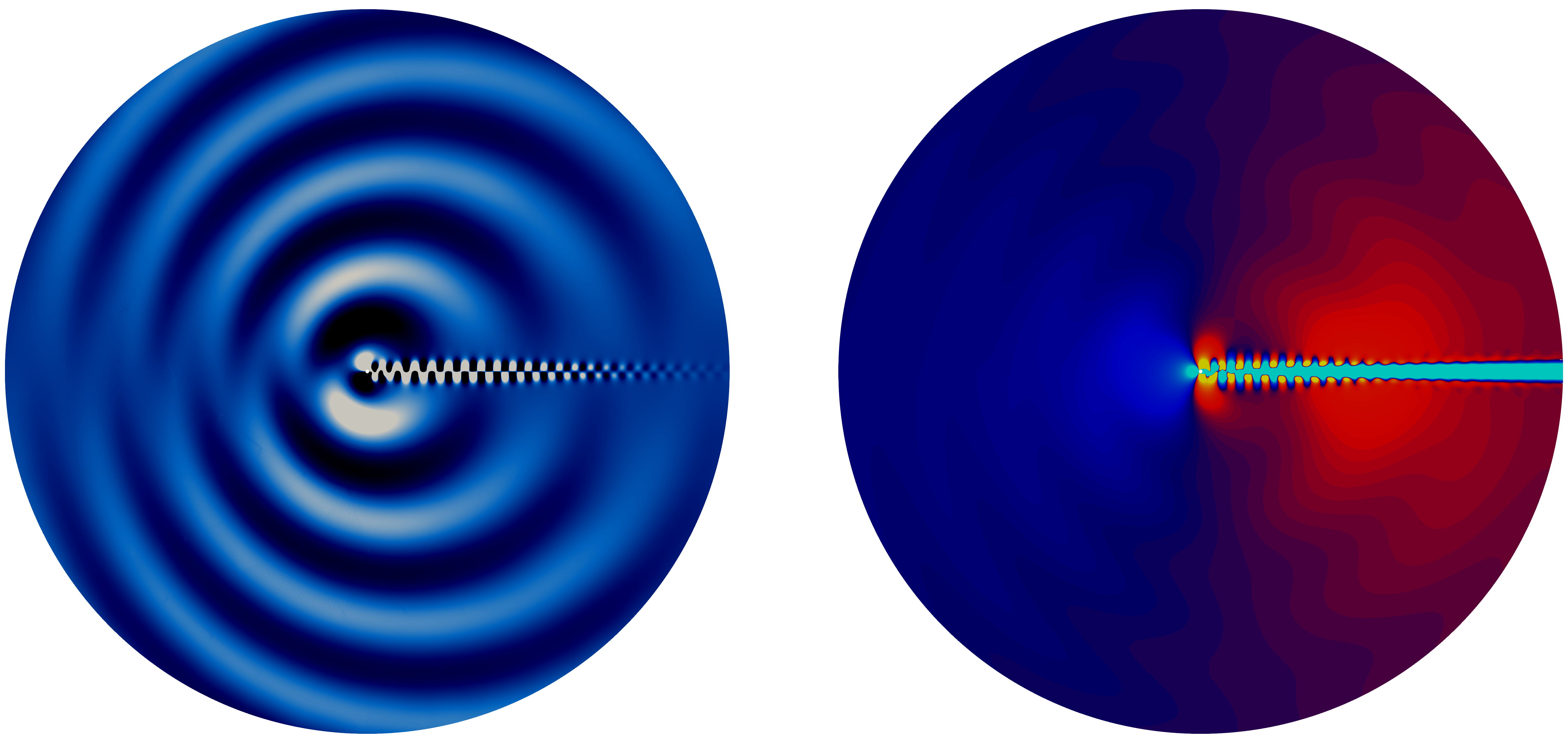
In the FWF research project P35931, High-Fidelity and Efficient Direct Aeroacoustic Simulations (DreAm), we focus on the numerical approximation of flow-induced acoustic waves. Our work explores the application of Hybrid Discontinuous Galerkin methods, with particular emphasis on developing accurate and efficient numerical fluxes—especially at artificial domain boundaries—and designing time-stepping schemes optimized for computational efficiency. Below you can see an example of an acoustic dipole that is induced by the flow around a small cylinder. 

The schmes are implemented in a Python module that is available on GitHub and is based on the Finite Element library NGSolve.