Numerische Analysis
In der Forschungsgruppe Numerische Analysis beschäftigen wir uns mit der Entwicklung, Analyse und Implementierung mathematischer Methoden zur numerischen Lösung von Problemen der Angewandten Mathematik. Dabei untersuchen wir zum Beispiel
- Verfahren für die numerische Differentiation und Integration.
- Methoden zum Lösen von (nicht-) linearen Gleichungssystemen.
Ein Schwerpunkt unserer Arbeit liegt auf der Fehler- und Konvergenzanalyse, die sicherstellt, dass die von uns entwickelten Verfahren zuverlässig und genau sind. Darüber hinaus betrachten wir strukturerhaltende Eigenschaften von Methoden um physikalische Prinzipien zu bewahren (zum Beispiel die Massenerhaltung bei inkompressiblen Fluiden). Ein wichtiges Anwendungsgebiet ist hierbei die Approximation von Lösungen partieller Differentialgleichungen (PDEs), die in vielen Bereichen der Natur- und Ingenieurwissenschaften auftreten, etwa:
- Mechanik und Materialwissenschaften
- Elektromagnetismus
- Strömungsmechanik
Ein bekanntes Verfahren zur numerischen Approximation von PDEs ist die Finite-Elemente-Methode (FEM). Dabei wird das zu untersuchende Gebiet in kleinere Teilgebiete (z. B. Dreiecke oder Tetraeder) zerlegt. Die nachfolgende Abbildung zeigt eine FEM-basierte Simulation des magnetischen Feldes welches durch eine Spule induziert wird (team7 benchmark).
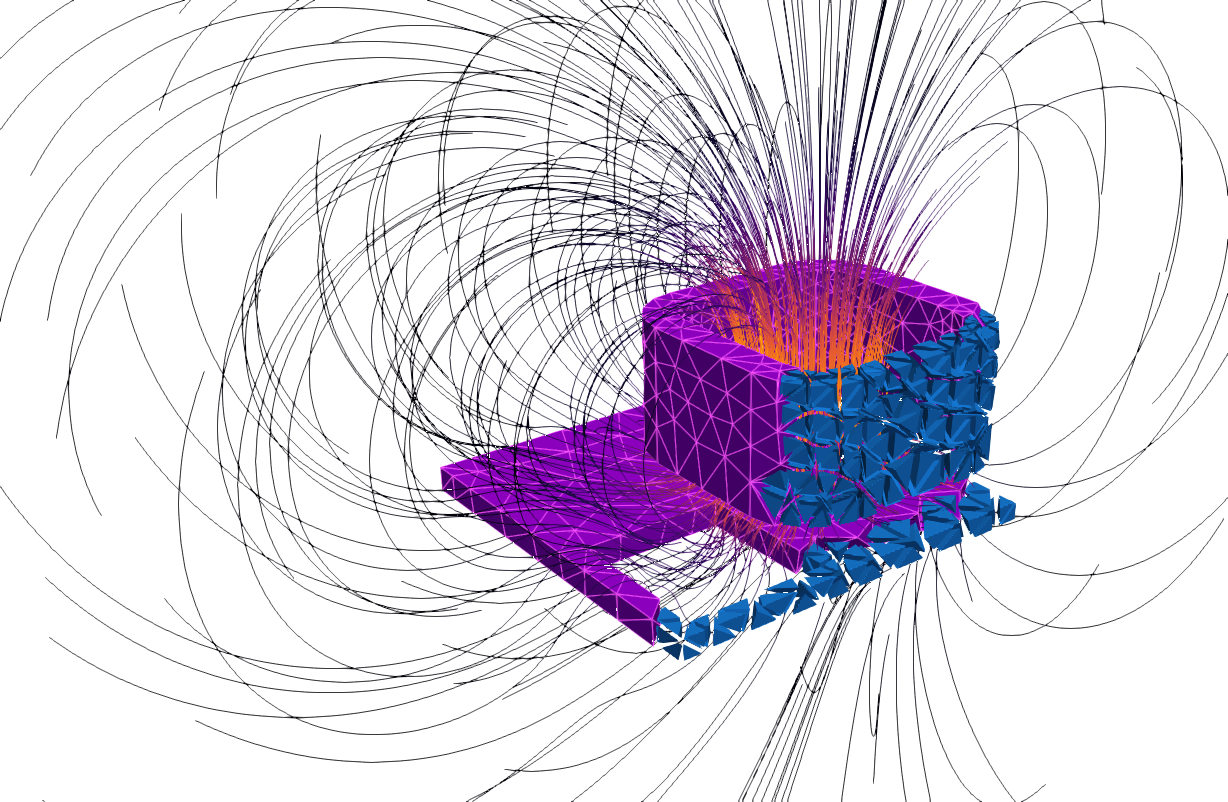
Auf diesen Teilgebieten entwickeln wir Varianten der FEM, die sowohl lokal als auch global eine hohe Genauigkeit bei der Lösung gewährleisten. Da die Anzahl der Freiheitsgrade bei komplexen Problemen sehr groß werden kann (106 und mehr), beschäftigen wir uns intensiv mit der Komplexitätsanalyse und der Optimierung von Algorithmen. Dies umfasst zum Beispiel
- Verfahren für große, dünnbesetzte oder schlecht konditionierte Matrizen,
- Optimierung numerischer Algorithmen für parallele Rechenarchitekturen und Supercomputer.
Zur praktischen Umsetzung nutzen wir unter anderem die Open-Source-Software NGSolve, die wir aktiv zur Implementierung und Analyse unserer Algorithmen einsetzen.
